Implementing InfoGAN: easier than it seems?

InfoGAN¹ is a really cool GAN (generative adversarial network)² variant. It is not only able to generate images, but can also learn meaningful latent variables without any labels on the data. One example given in the paper is that when InfoGAN is trained on the MNIST handwritten digit dataset, variables representing the type of digit (0-9), the angle of the digit, and the thickness of the stroke are all inferred automatically.

Here are some sample output images generated from my unofficial Torch implementation of InfoGAN. A 10-category salient variable was varied when generating these digits, shown horizontally. Whilst not perfect, notice that a lot of the digits are separated in a meaningful way without using any labels.

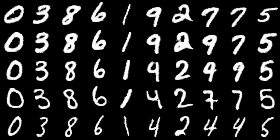
How does InfoGAN work?

The main InfoGAN proposal is to set aside part of the generator’s input $c$ as “salient”, in addition to the typical GAN noise input $z$. These salient latent variables can be sampled from any distribution you like - categorical, uniform, Gaussian, etc. The discriminator attempts to recover the salient variables by looking at the generated image, which is used to form a new “information regularization” term within the usual GAN objective function. So, instead of just outputting a prediction of whether the image is real or fake $\hat{y}$, the discriminator also has an output $\hat{c}$ for reconstructing $c$.

The authors of the paper take an information theoretic approach to explaining InfoGAN. More specifically, they state that InfoGAN works by maximizing the mutual information between the salient variables \(c\) and the generated images \(x\).

Let $C$ be a random variable representing the salient latent information and $X=G(C,Z)$ be a random variable representing the image produced by the generator from $C$ and noise $Z$. Using the definitions for mutual information, cross entropy, entropy, and conditional entropy, as well as the fact that KL divergence is non-negative, we get the following upper bound on mutual information:

This tells us that we can maximize the mutual information $I(C;X)$ by maximizing $\mathbb{E}_{X,C}[\log q(C|X)]$. That is, we want to minimize the negative log likelihood (NLL) of $q(C|X)$, our discriminator approximation of the true posterior distribution $p(C|X)$. In order to do this we need to be able to jointly sample from $C$ (easy since we defined the distribution of salient variables ourselves) and $X$ (also easy - generate noise to concatenate with the salient variables and do a forward pass through the generator). Just to reiterate, this is bog-standard GAN stuff - we just sample inputs to the generator and generate an image, which is exactly what you need to do with the usual GAN objective.

The only complicated stuff left is calculating the NLL for the salient variables. One way to do this is by going deep into defining random distributions and how to calculate the NLL for each. This is done in OpenAI’s implementation of InfoGan (see distribution.py). In a framework like Torch this means defining a new criterion, which is certainly possible, and I have done this in my unofficial Torch implementation of InfoGAN (see the pdist folder).

Do we even need special criteria?

I believe that we can simply use tried and true criteria like nn.MSECriterion and nn.ClassNLLCriterion instead of diving deep into custom NLL mumbo-jumbo. In fact, I have tried this and the results appear just as good. Why does this work? Well, let’s consider some distributions we could select for salient variables.

We define $c$ to be the input salient variables, and $\hat{c}$ to be the output predictions from our $q(C|X)$ approximation.

Categorical

Here we have $n$ discrete variables, of which one is set to 1 and the rest are 0. This is so-called “one-hot encoding”, and is used for usual classification problems.

This one is easy, since minimizing the NLL is what we do for classification anyway - it even says so on the tin (nn.ClassNLLCriterion). Just use this, it’s the same.

Gaussian

This one is a little trickier. First we will look at the definition for the NLL of a Gaussian:

Notice anything interesting? The only term involving $c$s is squared error with a scaling factor in front. If we use a fixed standard deviation, then minimizing the NLL of a Gaussian is equivalent to minimizing mean squared error. So we can simply use nn.MSECriterion!

Uniform

The official InfoGAN implementation treats uniform distributions as Gaussians for everything but sampling, so we can once again use MSE.

Conclusion

InfoGAN is really neat, and not nearly as difficult to implement as an initial read through of the paper might suggest. Essentially, we just need to make three adjustments to a regular GAN:

1. In addition to noise variables $Z$, sample some salient variables $C$ and provide these to the generator as part of the input.
2. Add a second head to the discriminator which predicts the salient variables. Something like a linear layer with number of outputs equal to the number of salient variable inputs is fine.
3. Use standard loss functions like MSE and discrete negative log likelihood on each variable in $c$ to calculate how well the discriminator is recognizing the variables from generated images. Add this to existing GAN loss, optionally scaling by some “information regularization coefficient” $\lambda$.

References